II. Linear Search

1. Search is one of the most basic things you do with a computer --- finding the item you want.
1. Data.
2. Algorithm.
3. Action
4. Actually, search is one of the most basic things you do, even without a computer!
5. Speeding up search is what computers are for.
2. How long does it take you to search for one item in data that isn't sorted?
1. Algorithm:  
1. Start at the beginning
2. Go to the end
3. Stop if you find an object that's key matches the one you are looking for.
2. Analysis (equally likely to be any item)
1. Best case: 1
2. Worst case: N
3. Average case: N/2
3. What if its sorted?
1. Algorithm:  
1. Start at the beginning
2. Go till you find the place your key should be.
2. Analysis (equally likely to be any item)
1. Best case: 1
2. Worst case: N
3. Average case: N/2
3. Not a big win!  And notice, sorting took us at least n log n time!
   
4. What if you are looking for K items with the same key?
1. Unsorted:  K*N
2. Sorted:  Probably just N+K
3. But both are O(N)

III. Binary Search

1. If you have a sorted list, you can do better than to go through from one end to another.
2. Think about how you might use a dictionary or a phone book (that doesn't have tabs!)
3. Clue:  try to think of a divide and conquer algorithm!
4. Algorithm
1. look in the middle of the list.
2. If that value is your key, you're done!
   
3. If your key is less than the current value, only consider the first half of the list, otherwise only consider the right side of the list.
4. Go back to 1 with your new (half-sized) list.
5. Example:  20, 35, 41, 48, 52, 76, 79, 84:   Find the value 79!
1. Center is 48 -- too little so go right
2. Center of right is 76 -- too little so go right.
3. Center of right of right is 79!  Done in 3 steps (list size of 8.)
6. Divide & Conquer should always give you log n performance.
7. In case anyone's not following, I'll do this one in pseudo code too, but really you should be able to write pseudo code (& real code!) by now from the description of the algorithm.

   integer key, sorta[]  // what we are looking for? & the sorted array (don't have to be ints...)
   boolean found         // have we found it?
   integer botIx, topIx  // bottom and top boundaries of the search
   integer midIx         // middle of current search
   integer locIx         // for storing the correct location if we find it
   
   botIx = 0, topIx = sorta.length - 1, locIx = -1, found = false;  // initialize
   while ((found == false) AND (botIx < topIx) do
   	midIx = (botIx + topIx) / 2; // returns the floor for ints
   	if (sorta[midIx] == key) {
   		found = true;
   		locIx = midIx;  // all done!
   		}
   	else if (key < sorta[midIx]) {
   		topIx = midIx - 1;
   		}
   	else  { // key > sorta[midIx]
   		botIx = midIx + 1;
   		}
   	} // end of while
   return locIx;  // will have value -1 if key was never found -- calling routine must handle this case!
   
   

8. This is a lot like the tree search I showed you Tuesday.  You are basically using pointer arithmetic to replicate a perfectly-balanced tree.
9. Note that we've done divide and conquer here without recursion, just with a loop & some arithmetic on the index values.  Of course, recursion is simpler: now from the description of the algorithm.
   

   if (key == self.key) return self;
   if (key < self.key) 
      if (not self.left) return null; 
      else return self.left.search(key)
   if (not self.right) return null; 
   else return self.right.search(key

10. what is the expected search time? (all three cases, both versions above)
    
11. Now if we are searching a lot more frequently than we are sorting, the cost of the initial sort may not matter much, because the fact we have a sorted list allows us to search in just log n time!
    

IV. Hash Sort & Search

1. Can we do even better than log n?  Yes, we can do constant time!
   
2. If you just use the key value as an array index, then you can sort in O(n) time and search in O(1) time.
3. What if you have more than one value for a single index?
1. Could make an array of lists, then search the list for the items you actually want.
2. If only a few ever have the same index, this is still O(1), but if only a few indecies shared by all items, becomes O(n).
1. That's a good indication you didn't choose a very good key!
2. (draw picture of this)
   
4. What if your keys are complicated values, e.g. words?
1. Could still make into an integer, e.g. treat the word as a base 26 number.
2. But the array would have to be really, really big!
3. Most of it would probably be empty.
4. Remember, using too much space slows you down too (swapping onto disk.)
5. A common solution is a data structure called a hash table.
1. Index is an array that's about the right size.
2. Need a cunning way to convert the keys into then index arrays.
1. This is called the hash function.
2. Lots of different functions are used for hash functions.
3. Should be something simple / fast so you can look things up quickly.
6. Take an example using modular arithmetic.
1. the mod is the remainder left over after an integer divide.
2. good hash function
1. division is pretty fast
2. can choose the denominator for the mod to be the size of the array.
7. List of values is  3, 10, 12, 20, 23, 27, 30, 31, 39, 42, 44, 45, 49, 53, 57, 60
8. Let's try hashing it into an array of size 15 (same size as list)

   0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
   30, 45, 60	31		3	49	20			23, 53	39	10		12, 27, 42, 57		44

   
   
9. Analysis
1. 10 items located in 1 step   = 10
   
2. 3 items in 2 steps              = 6
3. 2 items in 3 steps               = 6
4. 1 item in 4 steps                 = 4
   
5. So average time is (10 + 6 + 6 + 4 = 26) / 16 = 1.625 steps per retrieval
10. Because hashing functions are usually random with respect to the input, you can expect:
1. empty cells / wasted space
2. collisions (where more than one item tries to get in one cell)
1. have to make & search through list.  This is called chaining, and illustrated above.
   
2. wasted time!
3. Can use 2-dimensional array, but that wastes way more space, limits number of possible collisions
4. Can indicate you should use of new hash function if too many collisions (e.g. do mod 20, not mod 15)
   
11. More time efficient if less collisions, more space efficient if more collisions.
12. Normally people favor time, make the table sparse (that is, much larger than the data):
1. Still saves space over one big array indexed off keys.
2. If the table is sparse enough, can put collisions in the next open index.
1. Probably the simplest way to handle them.
2. This is called probing.
   
3. Let's try hashing it into an array of size 19 this time:

   0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
   57	20 [39]	39	3 [60]	23 [42]	42	44	45	27	60	10	30 [49]	12 [31]	31	49	53

4. Analysis
1. 12 items located in 1 step   = 12
2. 3 items in 2 steps              = 6
   
3. 1 item in 4 steps               = 4
4. 1 item in 6 steps               = 6
   
5. So average time is 28 / 16 = 1.75 steps per retrieval
5. You wouldn't really put the information in the square brackets in the table, I just did that to let you see where those numbers really wanted to be sorted originally.  The table really would look like this:

   0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
   57	20	39	3	23	42	44	45	27	60	10	30	12	31	49	53

6. Algorithm to search:
1. Derive a hash value mod tablesize from the search key, hashvalue.
2. Search for key starting at searchIx = hashvalue.
1. if sorta[searchIx] == null, then failed -- not in table.
2. if sorta[searchIx] == key, then succeeded.
3. otherwise, searchIx++, if searchIx > arraysize then searchIx =0 !! (wrap at the end!)
4. go back to 6.2.1
13. Analysis of Hash Search
1. Want to know how many items have to be searched to find a value.
2. As shown above, dependent on the load factor, A (really alpha, but HTML is lame.)
1. Like an array, the hash is constant on N.
   
3. A = number of occupied locations / table size
4. On average, probability of clash is 1 / (1 - A).
5. Successful search needs to examine (1 + 1 /(1 - A)) / 2 locations.
1. If you don't like just believing assertions (sensible), here's some more detailed notes.
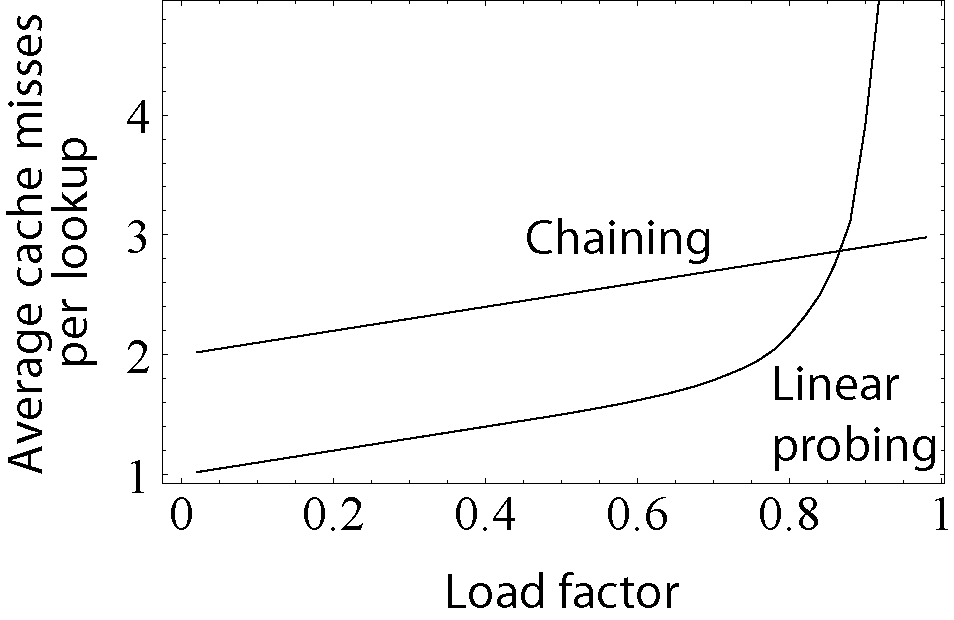
2. So for example, an 80% full table requires about 3 steps, irrespective of how large the table is!
6. Unsuccessful search needs to examine (1 + 1 / (1 - A)²) / 2.
7. So on an 80% full table, the average for an unsuccessful search is 13 steps, again regardless of table size.
8. The normal rule of thumb is never to let a table get more than 80% full.
1. Wikipedia has a nice illustration of why not.
2. 
   

V. Summary

1. Don't forget about linear & binary sorts!
2. Hashing is actually ubiquitous in computer science:
1. How do you think your variable names are stored?
2. Languages  like python & perl let you use strings as array indecies.
3. These are actually just hashes, like Java has, but they are disguised by the syntax (like java disguises the use of integer division with a /).